In mathematics, collinear points are defined as the points located on the same straight line. In contrast to lines, various planes may have overlapping points, but not vice versa. Collinearity is the property of three or more points in a plane near one another and can be connected via a straight line. The straight line will be the one path that connects the three or more congruent places.
Read on to learn more details on your question, ‘what are collinear points‘?
What are collinear points?
Collinearity is the property of points on a single line in geometry. Three or more points in a plane are collinear if they can be linked by a straight line of the same length. It is a grouping of points that share this trait. The points aligned in a line or row or the collinear points within a line are said to be “aligned.”
- Non-collinearity is defined as the property of three or more points that are not on a straight line. Non-collinearity occurs when no two points in a set share a line.
- Two points in a plane will always be collinear as a line, by definition, connects two points in space. However, there can only be a finite set of points between two points in a straight line.
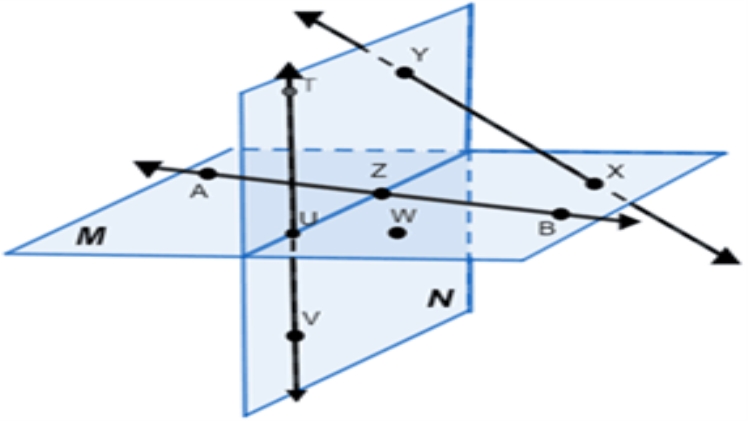
- Collinear points share their locations straight, but they need not be on the same plane. From fig. 1, you can see that some of the collinear points are co-planar (lying on the same plane), while some other points are connected in a straight line through different planes.
What are the methods used to determine if three points are collinear?
It is necessary to utilise the formula for collinear points to determine if three points are collinear or not. It is possible to determine if three points on a plane are collinear or not using different ways: Two formulae that are used for detecting whether two points are collinear or not are given below:
- The Formula for Slope
- The formula for the Area of a Triangle
Now, let us take a look at each of the formulas and examine them:
Slope method
The slope is the quality or value that determines the “steepness” or direction of a line. A slope indicates the rate of change of the gradient of a line. Since collinear points are on the same line, the slope between any two points must be equal. To determine whether a set of points are collinear, we can check whether the magnitude of their slopes is equal.
If (x1, y1) and (x2, y2) are two points in a plane, then the slope of the line connecting these two points shows the rate of change in y with every unit that the x covers.
That is, slope = .
Using this formula, we can determine whether the slopes of all three points coincide. If, upon calculation, the magnitude of the slope between two points is equal to that of another pair of points, then all of them are collinear points.
Solved Example:
Ex. Identify and demonstrate that the three-points P (4 and 6), Q (6 and 8) and R (10 and 12) are collinear in the coordinate plane.
Ans.
If the set of 3 points P (4 and 6), Q (6 and 8) and R (10 and 12) are collinear, then the slopes of the two pairs of points will be the same as the other.
We know, slope = .
For the line segment PQ, slope = = 1.
For line segment QR, slope = = 1.
For the line segment PR, slope = = 1.
From calculating the slope of the three-line segments, it’s clear that they all have an equal slope. Hence, they all fall within a straight line and are collinear.
Area of Triangle Method
If the area of a triangle formed by the three points is equal to zero, the points are collinear. This is because if all the points in the plane fall on the same line, they cannot form a triangle.
For this calculation, consider the coordinates of the three points as the coordinates of the edges of a triangle. The points will be collinear if the triangle’s area equals zero.
Solved Example:
Ex. Find whether the points S (0, 5), P (5, 10) and Q (15,20) are collinear using the formula for finding the area of a triangle.
We know area of a triangle formed by three points = ½ | x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2) |
Assigning the coordinates as different for the coordinates of a triangle, we get:
Area = ½ | 0 (10- 20) + 5 (20-5) + 15 (5-10) |
A = ½ x |0 + 5 x (-15) + 15 x (-5) | = 0.
Since, the area of the triangle is equal to 0, the points are collinear.
Important FAQs
- Define collinear points.
- Points that fall on the same straight line are called collinear points.
- What are the methods used to identify collinear points?
Ans. Slope method and area of a triangle method. Whenever the slopes of any two points are equivalent, three or more points are collinear. Combining the three points A, B, and C makes it possible to get three pairs of points: AB, BC, and AC. When the slope of AB matches that of the slopes of BC and AC, the points A, B, and C are collinear. Also, if the area of a triangle calculated using the three coordinates of the points is 0, then the points are collinear.
- What is an example of a collinear point in the real world?
Ans. There is collinearity amongst pupils who are seated at a long lunch table together. Rings on a shower curtain, rows of plants in a garden, digits on a ruler, moviegoers in a ticket wait, and commuters riding on a train are all examples of collinear items.
Conclusion
Collinearity is an important concept in mathematics and helps us situate properties associated with points in space. Three or more points are collinear if they all fall on a single line following the collinearity property. Those points which cannot be linked within a straight line are called non-collinear points. The formula for finding the area of the triangle or calculating slope can be used to find if a set of points are collinear.